Analytische Bedingungen für lineare Abhängigkeit für n Vektoren im n-dimensionalen Vektorraum

• - kanonische Basis des Vektorraumes

• - n Vektoren (=Anzahl der Dimensionen)

Vorbedingung ist lediglich, genauso viele Vektoren, wie der Vektorraum Dimensionen hat.

für allegilt: 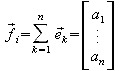für i = 1, 2, ..., n Gleichung (1)

Die Vektorensind als Linearkombinationen der Einheitsvektorendarstellbar.

a.) sind linear abhängig !

mit mindestens ein

:

können als Spalten einer Matrix aufgefasst werden!

( n, n )-Matrix

• daraus folgtdaraus folgt A hat eine Nullspalte, daraus folgt det A = 0

• Es ist mindestens ein weiteresdaraus folgt( die l-te Spalte von A ) ist ein Vielfaches der m-tem Spalte bzw. eine Linearkombination von anderen Spalten, daraus folgt

b.)sind linear unabhängig !

• bilden Basis von( Vektorraum mit n Dimensionen )

• für m = 1, ... , m Gleichung (2)

in (1) eingesetzt :

(1) in (2) eingesetzt :

Da dielinear unabhängig sind folgt daraus : Gleichung (3)

Fasst man dieals Werte einer Matrix 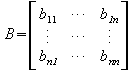dann entspricht (3)

daraus folgt : daraus folgt :

Zusammenfassung:

• gilt genau dann, wenn die Zeilen ( bzw. Spalten ) von A linear abhängig sind

• Die Vektorenbilden geanu dann eine Basis von, wennfür die Matrix A der Koeffizienten der Vektorengilt.