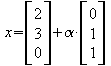Lösung
des inhomogenen Systems
Existenz einer Lösung
erweiterte
Koeffizientenmatrix
Satz:
Das inhomogene System
hat
genau dann eine Lösung, wenn
.
Beweis:
=>
Existenz einer Lösung
=> A und
haben
die gleiche Anzahl linear unabhängiger Spalten
=> b lässt sich
als Linearkombination der Spalten
von
A darstellen
=>
=>
ist
Lösung von
Es gibt eine
Lösung
von
=>
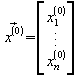
Es gilt
=>
=> b ist Linearkombination der Spalten von A
=> b kann zu
keinen
Beitrag leisten
=>
q.e.d.
Hinweis:
Es gilt
Beispiele:
=> keine Lösung ! ! !
Es
gibt keine Lösung, da die Ränge von A und
ungleich
sind.
Es gibt nur bei gleichen Rängen eine Lösung
=> es existiert mindestens eine Lösung ! ! !
=>
A = (n,n) - Matrix (quadratisch)
=> rg(A) = n => A regulär
=> es existiert eine eindeutige Lösung ! ! !
Bestimmung
einer speziellen Lösung
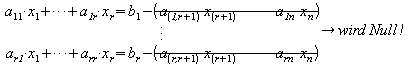
Man setzt
Zu lösen ist: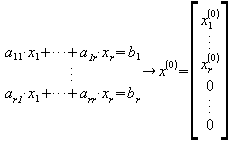
Beispiele:
rg(A)
= 1
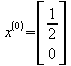
allgemeine Lösung :
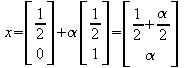
z.B. :
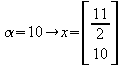oder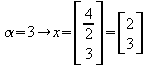
rg(A)
= 2
nur zwei Zeilen =>
=>
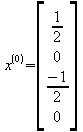
allgemeine Lösung :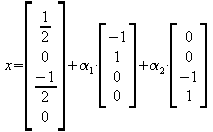
rg(A)
= 2
da nur zwei Zeilen =>
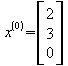
allgemeine Lösung :
