Gauß - Algorithmus
Einleitung
offene Probleme bei der praktischen Berechnung :
Berechnung der Determinanten
Berechnung der Inversen
Bestimmung des Ranges einer Matrix
Testen der Existenzbedingung des inhomogenen Systems
Bestimmung der Lösung des homogenen und inhomogenen Systems
Lösung : Gauß - Algorithmus [tadaaaa ! ! ! ]
Grundidee :
![]() wird
in ein System umgeformt, dass die gleiche Lösungsmenge besitzt,
aber eine wesentlich günstigere Form hat.
wird
in ein System umgeformt, dass die gleiche Lösungsmenge besitzt,
aber eine wesentlich günstigere Form hat.
günstige
Form :
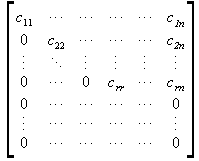 mit
mit![]() d.h.
untere Dreicksmatrix
d.h.
untere Dreicksmatrix
Sinn und Zweck des Gauß-Algorithmus ist es also, die Ausgangsmatrix irgendwie zu einer unteren Dreicksmatrix umzuformen.
Was ist eine Dreicksmatrix ?
Eine Dreicksmatrix ist eine Matrix bei der unterhalb bzw. oberhalb der Hauptdiagonalen alle Elemente gleich 0 sind. Die Hauptdiagonale ist in den unteren Beispielen gelb markiert, sie geht immer von links oben nach rechts unten. Selbstverständlich können die Einsen auch andere Werte annehmen, so auch die Null, das bedeutet, dass auch eine Diagonalmatrix (eine Matrix bei der nur die Elemente der Hauptdiagonalen ungleich Null sind, alle anderen sind Null ) eine spezielle Form der Dreiecksmatrix ist. Dasselbe gilt auch für die Nullmatrix ( eine Matrix die nur aus Nullen besteht ) [ keine Anspielung auf bestimmte Personen *g*]
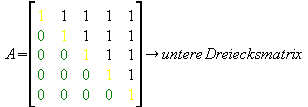
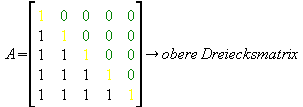
Der Gauß-Algorithmus
Der Gauß-Algorithmus erklärt sich am Besten mit Hilfe eines Beispieles.
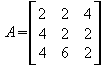
Diese Matrix A muss nun so umgebaut werden, dass sie am Ende eine untere Dreiecksmatrix ist. Hier nutzt der Gauß-Algorithmus die elementare Zeilenumformung als Werkzeug. Elementare Zeilenumformung bedeutet nichts weiter als, dass Zeilen beliebig mit frei gewählten Faktoren multipliziert und dividiert werden können. Weiterhin ist es auch erlaubt, dass man die Zeilen untereinander addiert und subtrahiert. Es dürfen auch Zeilen miteinander vertauscht werden (z.B. die erste mit der 3. Zeile usw.). Auch die Spalten dürfen untereinander getauscht werden, aber hier muss man sich merken welche Spalten man getauscht hat, da man sie am Ende der Berechnung wieder den entsprechenden Unbekannten zuordnen muss. Das bedeutet zum Beipiel, wenn x1 die Spalte 1 ist, x2 die Spalte 2 und ich vertausche sie, dann muss ich mir merken, dass beim Ergebnis x1 die Spalte 2 ist und x2 die Spalte 1. Alles andere ist nicht erlaubt.
Versuchen wir nun unsere Matrix A in eine untere Dreicksmatrix umzuformen. Am sinnvollsten ist es, als erstes unten links eine Null hinzubekommen. Bei unserem Beispiel ist das recht einfach.
3.Zeile = 3.Zeile - 2. Zeile
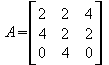
Nun ist es ratsam die 2. Zeile umzuformen, würde man versuchen die 3.Zeile weiter zu bearbeiten, dann würde die erste Null wieder zerstört werden.
2. Zeile = 2. Zeile - (2 * 1.Zeile)
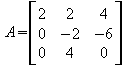
Jetzt fehlt nur noch eine Null.
3.Zeile = 3.Zeile + (2 * 2.Zeile)
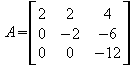
Fertig :-) !
Eigentlich gar nicht schwer. Es kommt zwar gelegentlich vor, dass man fürchterliche Zahlen herausbekommt, aber es funktioniert IMMER irgendwie ! Die Dreiecksmatrix ist die Basis für alle weiteren Berechnungen.
Berechnung der Determinanten
Wenn man die Determinante einer Matrix haben möchte, dann multipliziert man einfach alle Elemente in der Hauptdiagonalen der vorher berechneten Dreiecksmatrix. In unserem Beispiel bedeutet dies, 2 * -2 * -12 = 48, die Determinante ist also 48.
Normalerweise müsste man die Determinante wie unten beschrieben berechnen. Mit dem Gauß-Algorithmus geht dies jedoch wesentlich einfacher und schneller. Ausserdem ist so auch die Determinantenberechnung von grossen Matrizen möglich.
Determinante der unteren Dreiecksmatrix
![]()
Determinante der Ausgangsmatrix
![]()
Berechnung der Inversen
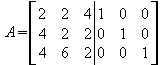
Um die Inverse zu berechnen muss man die Ausgangsmatrix nehmen und eine Einheitsmatrix danebenschreiben. Dann kann man beginnen die Ausgangsmatrix in eine untere Dreiecksmatrix umzuformen.
3. Zeile = 3. Zeile - 2.Zeile und gleichzeitig 2.Zeile = 2.Zeile - ( 2 * 1.Zeile )
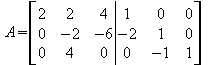
3.Zeile = 3.Zeile + ( 2 * 2.Zeile )
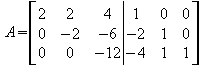
Danach ist man allerdings noch nicht fertig, denn jetzt beginnt man auch den oberen Teil der Dreicksmatrix in Nullelemente zu verwandeln. Hierbei geht man ähnlich vor wie bei den ersten Umwandlungen, muss allerdings darauf achten, die bereits bestehenden Nullen nicht wieder zu zerstören. Letzendlich erhält man eine Diagonalmatrix.
1.Zeile = 1.Zeile + ( 1/3 * 3.Zeile ) und gleichzeitig 2.Zeile = 2.Zeile - (1/2 * 3.Zeile )
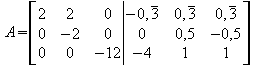
1.Zeile = 1.Zeile + 2.Zeile
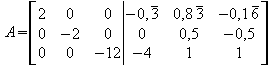
Der letzte Schritt bei der Berechnung einer Inversen Matrix ist es nun, die gesamte Matrix zeilenweise durch die entsprechenden Zahlen, die auf der linken Seite bestimmt werden, zu dividieren um auf dieser Seite eine Einheitsmatrix zu erhalten. Wie das gemeint ist, sieht man im Beispiel am Besten.
1.Zeile = ( 1.Zeile / 2 ) und 2.Zeile = ( 2.Zeile / -2 ) und 3.Zeile = ( 3.Zeile / -12 )
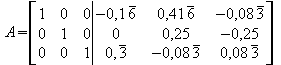
Was jetzt auf der rechten Seite steht sieht zwar bescheiden aus ist aber tatsächlich die Inverse Matrix zu der Ausgangsmatrix.
D.h. Neben die Ausgangsmatrix eine Einheitsmatrix schreiben, Ausgangsmatrix zu Einheitsmatrix umformen, rechte Seite ist Inverse Matrix zur Ausgangsmatrix.
Bestimmung des Ranges einer Matrix
Ausgangspunkt für die Bestimmung des Ranges einer Matrix ist wieder die Dreicksmatrix.
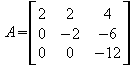
Wenn die Ausgangsmatrix in eine Dreicksmatrix umgeformt ist, werden alle Nullzeilen weggestrichen (in unserem Beispiel gibt es keine, also wird auch nichts weggestrichen) und die Anzahl der verbleibenden Zeilen ist der Rang. Die Matrix in unserem Beispiel hat also den Rang 3. Auch ganz einfach.
Testen der Existenzbedingung des inhomogenen Systems
Was ist ein inhomogenes System ?
Ein inhomogenes System ist ein System dessen Gleichungen ungleich Null sind.
Die Existenzbedingung eines bestehenden Systems testen bedeutet lediglich, dass man die Matrix wie üblich erstellt, allerdings eine weitere Spalte mit den Ergebnissen der Gleichungen hinzufügt. Diese Matrix wird nach dem bekannten Muster in eine Dreiecksmatrix umgeformt. Sollten dann in der letzten Zeile überall nur Nullelemente stehen, mit Ausnahme der Ergebnisspalte, ist dieses System nicht existent. Dies erklärt sich dadurch, dass diese Gleichung bedeuten würde Null multipliziert mit irgendetwas ergäbe etwas was ja nach Adam Riese nicht möglich ist.
Bestimmung der Lösung des homogenen und inhomogenen Systems
Lösen des homogenen Systems
Ein homogenes
Gleichungssystem wird wie folgt gelöst: Man nimmt die umgeformte
Dreiecksmatrix und bestimmt genausoviele Unbekannte wie es fehlende
Gleichungen gibt. Diese Unbekannten dürfen allerdings nicht alle
gleich Null sein. In Normalfall empfielt es sich, genau eine
Unbekannte mit Eins zu bestimmen. Diese Werte setzt man dann
nacheinander in die Dreicksmatrix ein um die restlichen Unbekannten
herauszubekomm en. Jede der Unbekannten muss einmal auf Eins gesetzt
werden. Wenn man zum Beispiel drei fehlende Gleichungen hat benutzt
man die letzten drei Unbekannten. Da man drei Ergebnisse benötigt
setzt man jeweils zwei der Unbekannten auf Null und die dritte auf
eins. Diese drei Ergebnisse hintereinander geschrieben und
mit![]() verknüpft
bedeuten das Ergebnis :
verknüpft
bedeuten das Ergebnis :
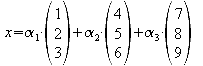
Lösen des inhomogenen Systems
Für die Lösung des inhomogenen Gleichungssystems gibt es zwei unterschiedliche Vorgehensweisen. Für beide Methoden ist die Vorraussetzung eine umgeformte Dreicksmatrix, welche die Existenzbedingung erfüllt.
Im ersten Fall ist der Rang der Matrix entsprechend der Anzahl der Unbekannten des Gleichungssystems. Hier gibt es lediglich eine eindeutige Lösung, deren Bestimmung ähnlich dem homogenen System verläuft. Man kann in der letzten Zeile sehr schnell den Wert der letzten Unbekannten erkennen. Dieser Wert wird dann in die darüberliegende Zeile eingesetzt, woraus sich der Wert der vorletzten Unbekannten ergibt. Diese Systematik wird einfach so lange weitergeführt, bis alle Unbekannten einen bestimmten eindeutigen Wert haben.
Im zweiten Fall ist das Gleichungssystem unterbestimmt und somit nicht eindeutig lösbar. Es wird hierfür dann die Lösung des homogenen Gleichungssystems plus die Lösung des inhomogenen Systems verwendet. Ich gehe hierbei davon aus, dass die Lösung des homogenen Systems bereits wie oben besprochen berechnet wurde. Für die noch fehlenden Unbekannten wird einfach Null eingesetzt und die Werte Wie im ersten Fall berechnet. Die beiden Lösungen werden additiv verknüpft. Und wie beim homogenen System dargestellt.