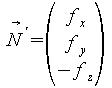Vektorprodukt ( äußeres Produkt, Kreuzprodukt )

Nur im( 3-dimensionalen Raum definiert ) :

Definition:

Das Kreuzprodukt zweier Vektoren ist definirt als: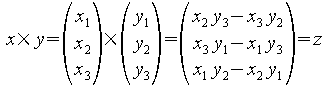

Schreibweise:

Eigenschaften des Vektorprodukts:

1. und"Rechtssystem"

   Beweis:

   

2. Das Vektorprodukt ist nicht assoziativ, d.h.

3. Das Vektorprodukt ist nicht kommutativ, d.h.

4. Das Vektorprodukt ist schief kommutativ, d.h.

5. Es gilt für, dann giltwobeider Winkel ist, den x und y einschliessen

6. wobei A der Flächeninhalt des von x und y aufgespannten Parallelogramms ist.

7. Distributivgesetz:

   

Verwendungen:

• Drehmoment:

  • r gleich dem Abstand Drehpunkt - Angrifspunkt

  • F gleich dem Kraftvektor

• undsind Vektoren in der Tangentialebene, d.h.

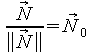• nennt man normierten Normalenvektor, d.h. ein Normalenvektor mit der Länge 1

• Flächenpunkt:

• Flächengleichung:

Daist gibt es natürlich pro Vetorenpaar zwei Normalenvektoren.

Es gilt: Wenn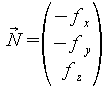dann ist