,
auf der Gerade
.
Analytische Geometrie des Raumes
Gerade im Raum
a)
Gegeben sei P mit drei Koordinaten,
auf der Gerade.
Ortsvektor
.
Geradengleichung
mit
gleich
dem Vektor, der die Richtung der Geraden festlegt.
beliebig
b) Gegeben
sind
und
auf
der Gerade:
Ebene im Raum
a) eindeutig
bestimmt durch einen Punkt
und
zwei linear unabhängige Vektoren, die in der Ebene liegen (
keine kollinearen Vektoren !!! )
mit
beliebig.
b)
PARAMETERGLEICHUNG:
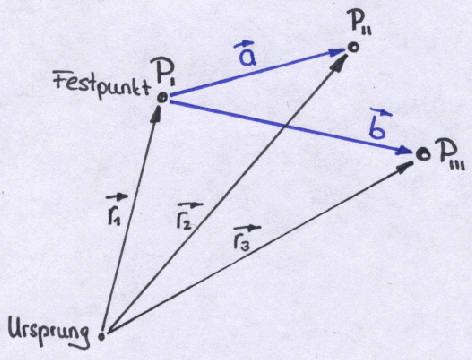
Die Ebene wird eindeutig durch 3 kolineare Punkte P1,P2,P3 definiert.
Die Parametergleichung besteht aus einem Festpunkt
,
und zwei Richtungsvektoren
,welche
die Ebene aufspannen. Der Festpunkt ist der Ortsvektor von P1
. Die Richtungsvektoren erhält man, indem man die
Differenz zwischen den anderen Ortsvektoren bildet: z.B.
Die folgenden drei Punkte spannen eine Ebene E auf, deren Parametergleichung aufgestellt werden soll.
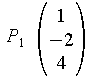
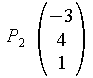
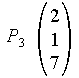
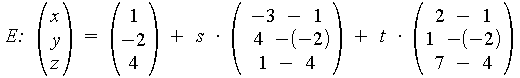
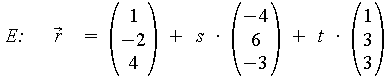
Man kann diese Gleichung auch als KOORDINATENGLEICHUNG schreiben:
Nun kann man die Gleichungen so zusammenfassen, dass die Parameter s und t entfallen.
So erhält man die kartesische Form der Ebenengleichung (auch allgemeine Form genannt).
c) KARTESISCHE
GLEICHUNG:
Für
obiges Beispiel lautet sie:
Aus dieser Gleichung kann man mühelos den Normalenvektor ablesen:
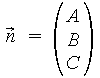also für obiges Beispiel:
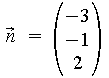
Man
erhält den Normalenvektor ebenfalls durch das Kreuz- bzw.
Vektorprodukt der beiden Richtungsvektoren
und
.
(siehe e)
d)
IMPLIZITE GLEICHUNG:
Mit dieser Form lässt sich leicht herausstellen, ob sich ein Punkt Px auf der Ebene befindet. Man setzt die
Koordinaten des Punktes für x,y und z ein.
Ergebnisinterpretation:
der Punkt Px befindet sich auf der
betrachteten Ebene
der Punkt Px befindet sich nicht auf der Ebene, das
Vorzeichen gibt an, dass er auf der „negativen“ Seite der
Ebene liegt.
der
Punkt Px befindet sich nicht auf der Ebene, das Vorzeichen
gibt an, dass er auf der „positiven“ Seite der Ebene
liegt.
Anmerkung: positiv und negativ bezeichnen hier nur die beiden Seiten, da jede Ebene den Raum in zwei Hälften teilt. Ob das Ergebnis positiv oder negativ ist, hängt letztendlich von der Orientierung des Normalenvektors ab.
Beispiel:
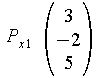
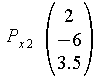
e) HESSE'SCHE NORMALFORM:
Herleitung ausgehend von der Parametergleichung:
Subtraktion von
skalare Verknüpfung mit dem Normalenvektor
Man normiert den Normalenvektor zum Einheitsnormalenvektor, indem man ihn durch seinen Betrag dividiert.
Der Einheitsnormalenvektor
hat den Betrag 1.
HESSE'SCHE
NORMALFORM:
Ausmultipliziert
erhält man:
allgemeiner
Teil, da
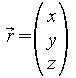
reeller
Teil
f) ACHSENABSCHNITTSFORM:
Diese Gleichung zeigt die Schnittpunkte mit den Koordinatenachsen.
Die kartesische Form lässt sich einfach in die Achsenabschnittsform umwandeln: man dividiert durch D. Unter Verwendung der Doppelbruchregeln erhält man dann unter dem Bruchstrich die Koordinaten.
Bedingung:
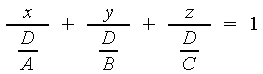oder
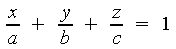
Man kann es auch anders rechnen:
x-Achse:
y-Achse:
z-Achse:
Beispiel zur Bildung der Achsenabschnittsform:
kartesische
Gleichung:
Dividieren
durch
Achsenabschnittsform:
Kehrwert
nehmen:
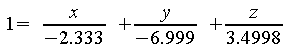
Die Achsen werden also an folgenden Stellen durchbrochen:
x-Achse: [-2.333/0/0]
y-Achse: [0/-6.999/0]
z-Achse: [0/0/3.4998]
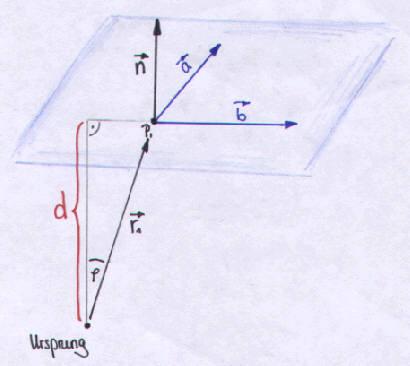
Abstand der Ebene vom Ursprung:
d ist der Abstand vom Ursprung
(entfällt
somit)
ist
der Winkel zwischen
und
Anmerkung: die Hessesche Normalform ist bis auf das Vorzeichen von d eindeutig, auch hier kommt es auf die Orientierung des Einheitsnormalen- vektors an.
Die Herleitung der Hesseschen Normalform und die Berechnung des Abstandes der Ebene E vom Ursprung soll nachfolgend am Beispiel verdeutlicht werden:
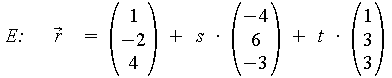Parametergleichung
Bilden des Normalenvektors: Kreuzprodukt der Richtungsvektoren
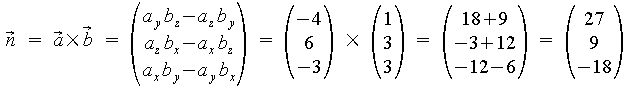
Normieren zum Normalenvektor:
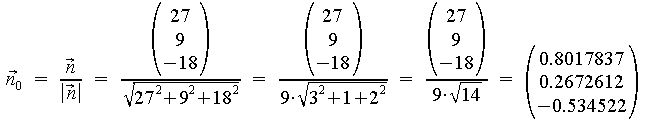
Abstand der Ebene E vom Ursprung:
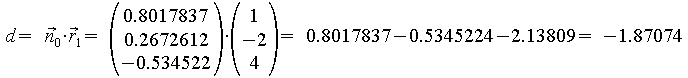
UMWANDLUNG DER HESSESCHEN NORMALFORM IN DIE KARTESISCHE FORM:
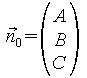
Zusatz:
Man kann auch mit dem Normalenvektor anstatt des Einheitsnormalenvektors rechnen, dann ergibt sich folgende Form:
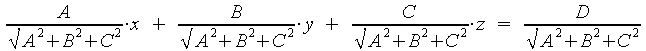
Dies ist eine andere Gleichung der hesseschen Normalform.
Beispiel zur Umwandlung in die kartesische Form:
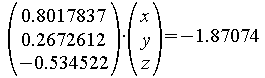
