Stetige Funktionen
Abbildungen und Funktionen
Definition:
Es seienM und N Mengen.
Eine Abbildung f von M in N ist eine Vorschrift, durch die jedem
Element![]() zugeordnet
wird. N wird Zielmenge genannt und M Definitionsmenge
zugeordnet
wird. N wird Zielmenge genannt und M Definitionsmenge
Schreibweise:![]()
Definition:
Eine Abbildung![]() mit
mit![]() heißt
(reelle) Funktion.
heißt
(reelle) Funktion.
![]() -
Definitionsbereich
-
Definitionsbereich
![]() bzw
bzw![]() -
Zuordnungsvorschrift
-
Zuordnungsvorschrift
![]() -
Argument; unabdingbare Variable; Urbild von y
-
Argument; unabdingbare Variable; Urbild von y
![]() bzw
bzw![]() -
Bild von x unter f; abhängige Variable; Wert der Funktion an der
Stelle x
-
Bild von x unter f; abhängige Variable; Wert der Funktion an der
Stelle x
![]() -
Wertebereich der Funktion f;
-
Wertebereich der Funktion f;![]()
Beispiele für Abbildungen und Funktionen
![]()
![]()
Abbildung f: M -> N
ist definiert durch:![]()
![]()
![]()
![]()
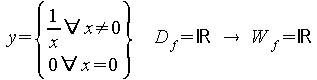
![]()
Nicht jede Zuordnungsvorschrift definiert eine Funktion:
![]() keine
Funktion, denn x = 1 => y = 1 und y = -1
keine
Funktion, denn x = 1 => y = 1 und y = -1
![]() Kreisgleichung
( keine Funktion )
Kreisgleichung
( keine Funktion )
![]() keine
Funktion, da für x = 0 nicht definiert
keine
Funktion, da für x = 0 nicht definiert
Funktion falls![]()
![]() keine
Funktion
keine
Funktion
Funktion falls![]()
Definition:
Die Menge aller Punkte
(x,y) mit![]() und
und![]() heißt
Graph der Funktion f
heißt
Graph der Funktion f
Beispiele:
![]()
![]()
Signumfunktion:
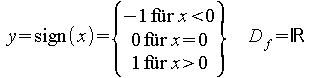
Nebenbemerkung:
Lineare Abbildungen:
Eine Abbildung f: M->N
heißt linear (Homomorphismus) wenn für alle![]() und
und![]() gilt:
gilt:
![]()
![]()
Dies gilt nach dem ersten Gefühl für alle Geraden, was aber nicht der Fall ist, da bei Geraden mit Achsenabschnitten die Bedingungen nicht mehr erfüllt werden. D.h. nur Ursprungsgeraden sind lineare Funktionen !!!
Affine Abbildungen:
Eine affine Abbildung ist eine Abbildung, die sich aus einer linearen Abbildungund einer Translation (Achsenabschnitt) zusammensetzt.
Allgemeine Geradengleichung y = mx + b beschreibt eine affine Abbildung !
Definition:
Umkehrfunktion ( inverse Funktion )
Eine Funktion
![]() mit
mit![]() und
und![]() ,
die jedem
,
die jedem![]() genau
das
genau
das![]() zuteilt,
für welches
zuteilt,
für welches![]() gilt,
heißt Umkehrfunktion von
gilt,
heißt Umkehrfunktion von![]()
Schreibweise:![]()
Beispiele:
![]()
![]()
![]()
![]() keine
Funktion, da
keine
Funktion, da![]() immer
zwei Werte zugeordnet sind => nicht umkehrbar
immer
zwei Werte zugeordnet sind => nicht umkehrbar
Satz:
Eine Funktion![]() ist
genau dann umkehrbar, wenn jedes
ist
genau dann umkehrbar, wenn jedes![]() höchstens
einmal als Bild eines
höchstens
einmal als Bild eines![]() auftritt,
d.h. aus
auftritt,
d.h. aus![]()
![]()
![]()
Umkehrfunktion bedeutet graphisch: Spiegelung an y = x