A[4/1] B[2/3]Übungen zur Analysis [Januar 2002]
Bestimmen sie die Parameterder folgenden Funktionen, welche diese Punkte durchlaufen.
Gleichungen subtrahieren
2.
A[4/1]
B[2/3]
Gleichungen
subtrahieren
3.
A[4/1]
B[2/3]
Gleichungen dividieren
5.
A[4/1] B[2/3]
a
isolieren
Bestimmen Sie mittels Kurvendiskussion den Graph dieser Funktionen.
1.
Definitionsbereich:
Symmetrie:
keine
Symmetrie vorhanden
Schnittpunkt
y-Achse: x=0
y=5
Nullstelle:
y=0
x=5
Verhalten
im Unendlichen:
lokale
Extrema:
hinreichende
Bedingung nicht erfüllt, es gibt keine Extrema, da nur
linear
Monotonie:
f(x) ist streng monoton fallend
Keine Wendepunkte oder Polstellen vorhanden.
Graphische Darstellung:
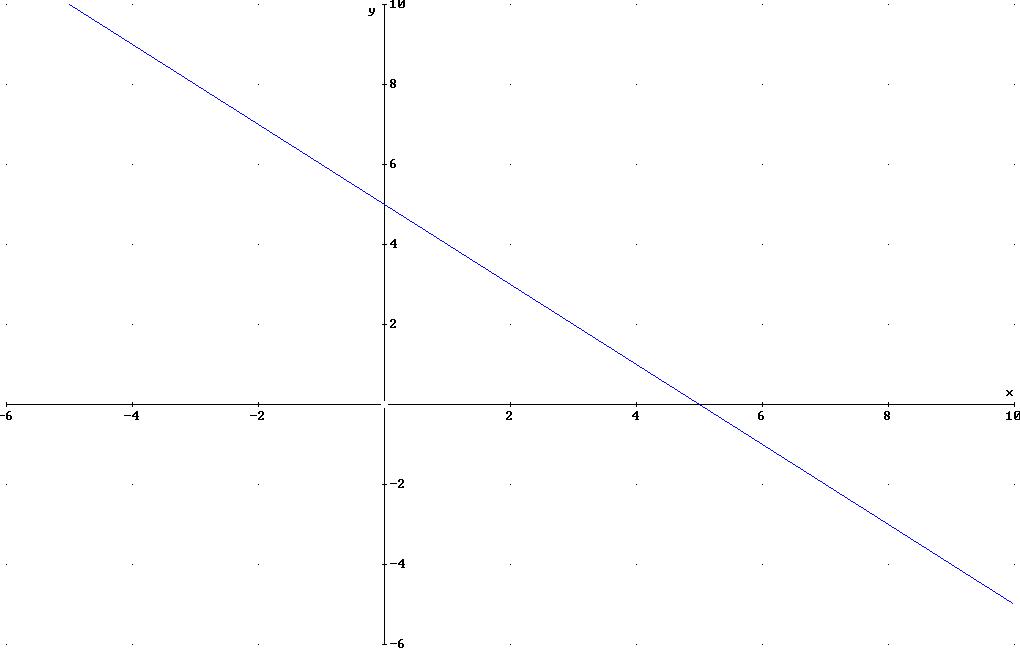
2.
Definitionsbereich:
Symmetrie:
keine
Symmetrie
Schnittpunkt
mit der y-Achse: s=0
y= +10.5
Nullstellen:
y=0
x1=3.5
x2=3
Verhalten
im Unendlichen:
lokale
Extrema:
EP [3.25/-0.125]
Minima
Monotonie: s1=0 s2= EP=3.25 s3=6
f(s1)=10.5 > f(s2)=-0.0625 < f(s3)=7.5
monoton
fallend
monoton
steigend
Wendestellen:
hinreichende
Bedingung nicht erfüllt
Es sind keine Wende- oder Polstellen vorhanden.
Graphische Darstellung:
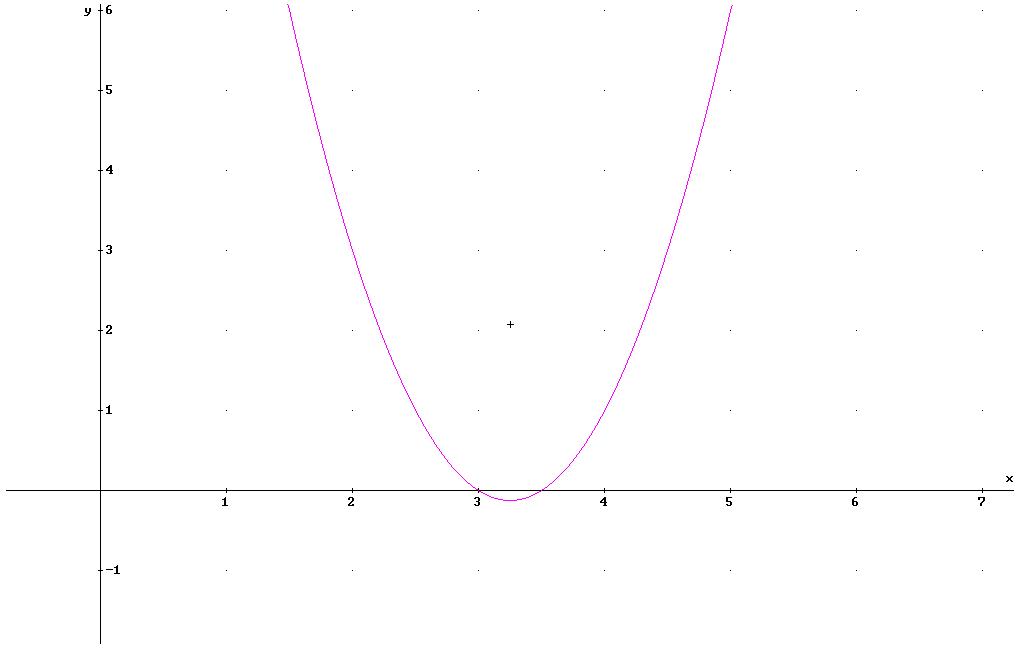
3.
Definitionsbereich:
Symmetrie:
keine
Symmetrie
Schnittpunkt
mit der y-Achse: x=0
y=9
Nullstellen:
y=0
|:9
|
| ln
ln
von 0 ist n.d.
keine
Nullstellen
Verhalten
im Unendlichen:
lokale
Extrema:
|
| ln
ln
von 0 ist n.d.
keine Extremstellen
Monotonie: im Bereich x1=-1 bis x2=6
monoton fallend
Es sind keine Wende- oder Polstellen vorhanden.
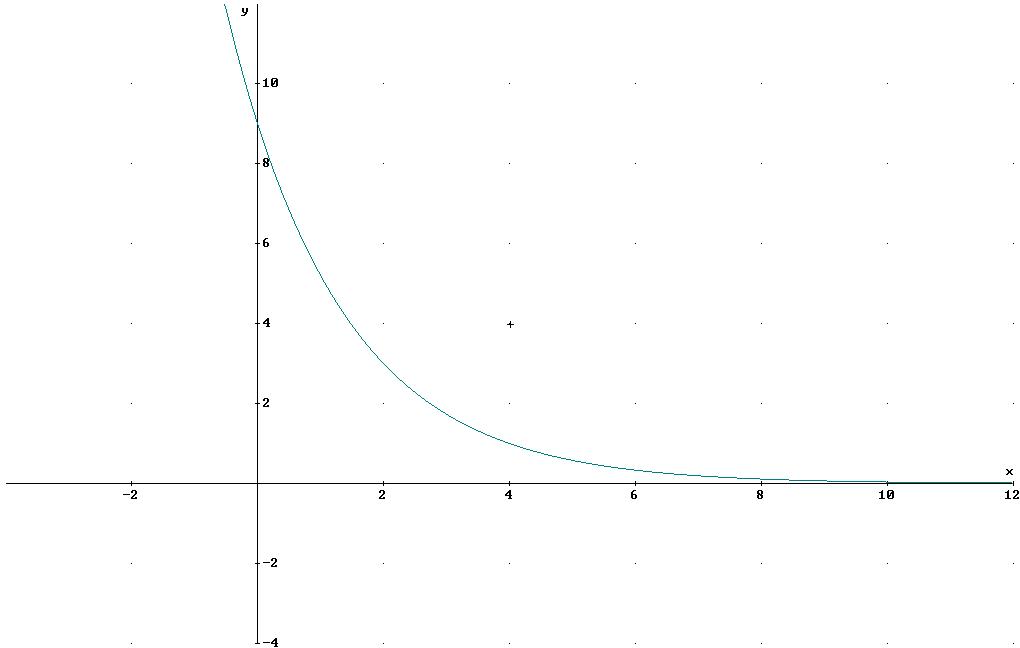
4.
Definitionsbereich:
Symmetrie:
keine
Symmetrie
Schnittpunkt
mit der y-Achse: x=0
ln
von 0 n.d.
Kein
schnittpunkt
Nullstellen:
y=0
x2=4.598
Verhalten
im Unendlichen:
lokale
Extrema:
EP
[ 1.6903304 / 3.048289 ]
|
| (-a)
| e
| :c
Maxima
Monotonie: x1=0.1 x2=1.69 x3=4
l(x1)=0.69 < l(x2)=3.05 > l(x3)=2.75
monoton
wachsend
monoton
fallend
Wendestellen:
hinreichende
Bedingung nicht erfüllt!
Keine Wende- oder Polstellen vorhanden.
Graphische Darstellung:
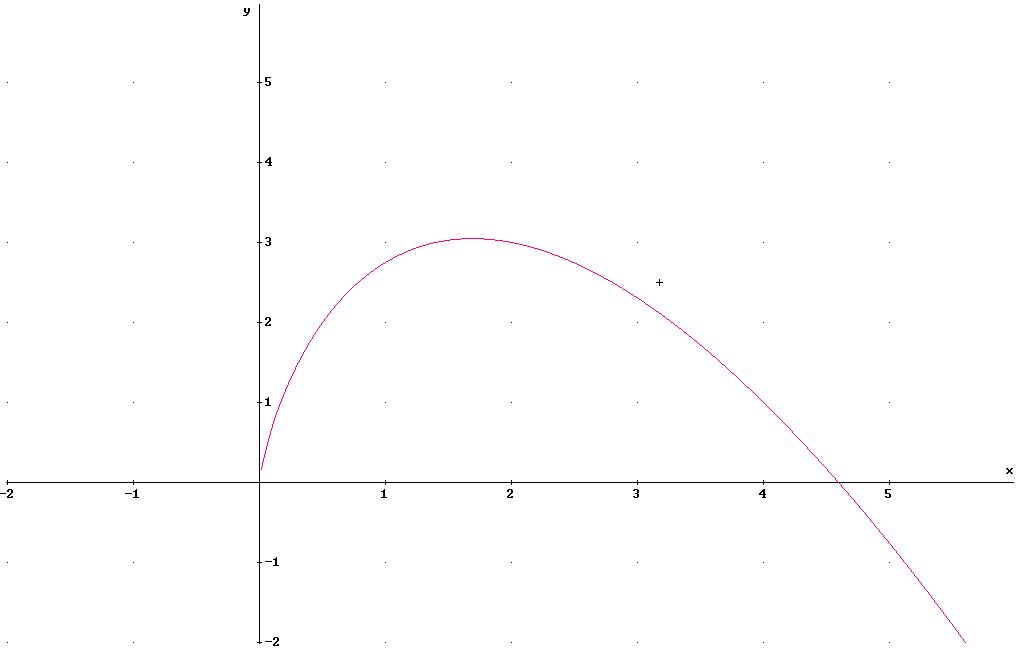
5.
Definitionsbereich:
Definitionslücken:
Nenner=0
x1= 1.069045 x2= -1.069045
Zähler
!
hinreichende
Bedingung erfüllt
Symmetrie:
keine
Symmetrie
Schnittpunkt
mit der y-Achse: x=0
y=-2
Nullstellen:
y=0
x0=
-0.727272
Verhalten
im Unendlichen:
lokale
Extrema:
keine lokalen Extrema
|:
einsetzen
in p-q-Formel
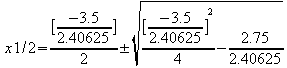
negative
Wurzel=n.d.
Monotonie: x1=-5 x2=-1.07 x3=1.07 x4=5
monoton
fallend
monoton
fallend
monoton
fallend
monoton
fallend
Wendestellen:
ABLEITUNGEN:
2.Ableitung Null setzen (es wird nur der Zähler benötigt).
|:
4.2109
Suchen
der Nullstelle durch Probieren: x=0
0.831176
x=-0.5
-0.462665
Erste
Schätzung: xo= -0.3
-0.028039
NEWTON'SCHES
NÄHERUNGSVERFAHREN:
x1= -0.2874887
x2= -0.2883391
x3= -0.2883393
Die
dritte Näherung bringt bereits eine Übereinstimmung bis auf
sechs Stellen hinter dem Komma.
x=
-0.288339
POLYNOMDIVISION: Weitere Nullstellen suchen.
=
Erhaltene
quadratische Gleichung nach p-q-Formel lösen:
negative
Wurzel ist nicht definiert!
Es sind keine weiteren Nullstellen, also auch keine weiteren Wendestellen vorhanden. Für die erhaltene Nullstelle bei x= -0.288339 ist nun die hinreichende Bedingung zu prüfen.
hinreichende
Bedingung erfüllt!
Die Wendestelle befindet sich bei WP [-0.288339/-1.3017674]
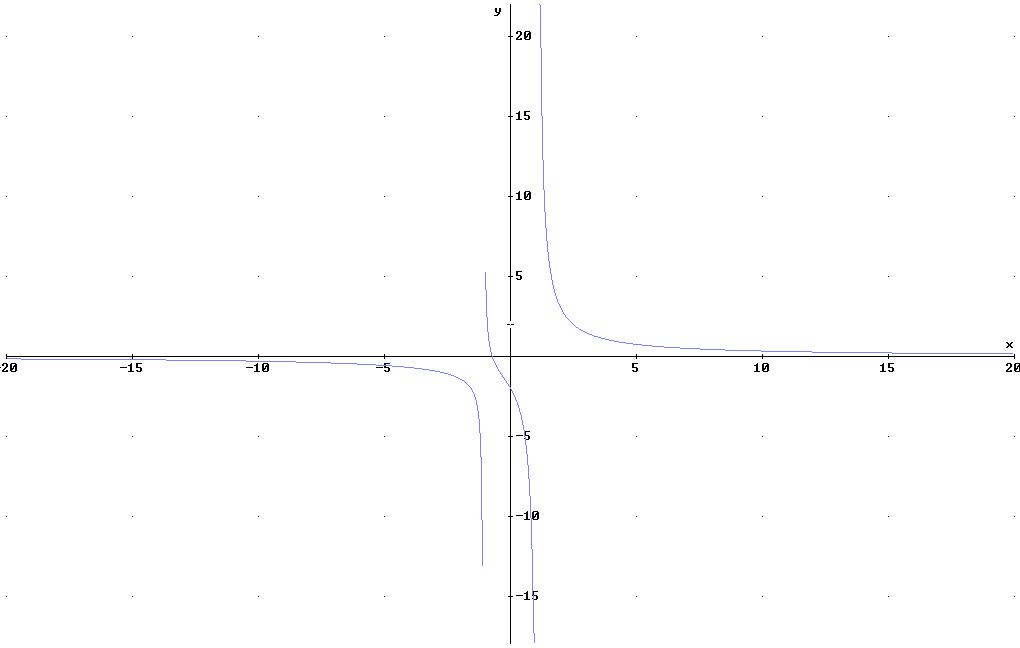
Graphische Darstellung:
Bestimmen Sie die Gleichungen der Tangenten und der dazu senkrechten Geraden durch den Punkt [4/1] für alle diese Graphen.
1.
Tangentengleichung:
Orthogonalengleichung:
2.
Tangentengleichung:
Orthogonalengleichung:
3.
Tangentengleichung:
4.
Tangentengleichung:
Orthogonalengleichung:
Tangentengleichung:
Orthogonalengleichung:
Die Funktion f(s) hat an allen Stellen s mit s>0 je eine Tangente. Geben Sie die Gleichung dieser Tangentenschar an.
Ausgangsgleichung
(2.Aufgabe)
Erste
Ableitung = Anstieg der Tangente
Tangentengleichung
y entspricht f(s) ,
x entspricht s
nach n umgestellt
n durch obigen Ausdruck ersetzt
Ausdrücke für f(s) und f'(s) einsetzen
zusammenfassen
Einsetzen von a für s als üblicher Parameter
Gleichung der Tangentenschar
Graphische Darstellung:
Gleichungen dividieren
Orthogonalengleichung: