Kurvendiskussion

Folgende Funktion soll nach allen Kriterien untersucht und anschließend dargestellt werden.

Definitionsbereich:

Nenner Null setzen:

Zähler prüfen: ,

Die Funktion ist an den Stellen x=2 und x=-2 nicht definiert.

mit

Verhalten an den Polgeraden:

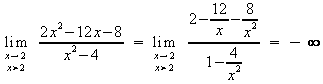
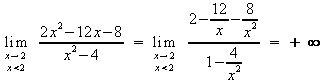
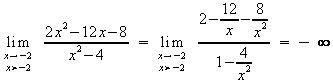
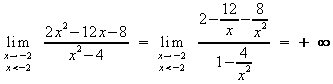
Achsenschnittpunkte:

Y-Achse: x=0 ASP [0/2]

X-Achse: y=0 nach p-q-Formel lösen

PX1 [6.6055/0]

PX2[-0.6055/0]

Ableitungen:

=

=

=

=

lokale Extrema:

keine Extrema

Wendestellen:

keine Lösungen

hinreichende Bedingung für x1 prüfen:

Wendestelle bei WP [0/2]

Verhalten im Unendlichen:

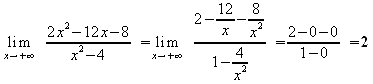
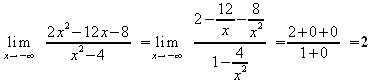
Monotonieverhalten: x1=-2.1 x2=0 x3=2.1

Symmetrien:

G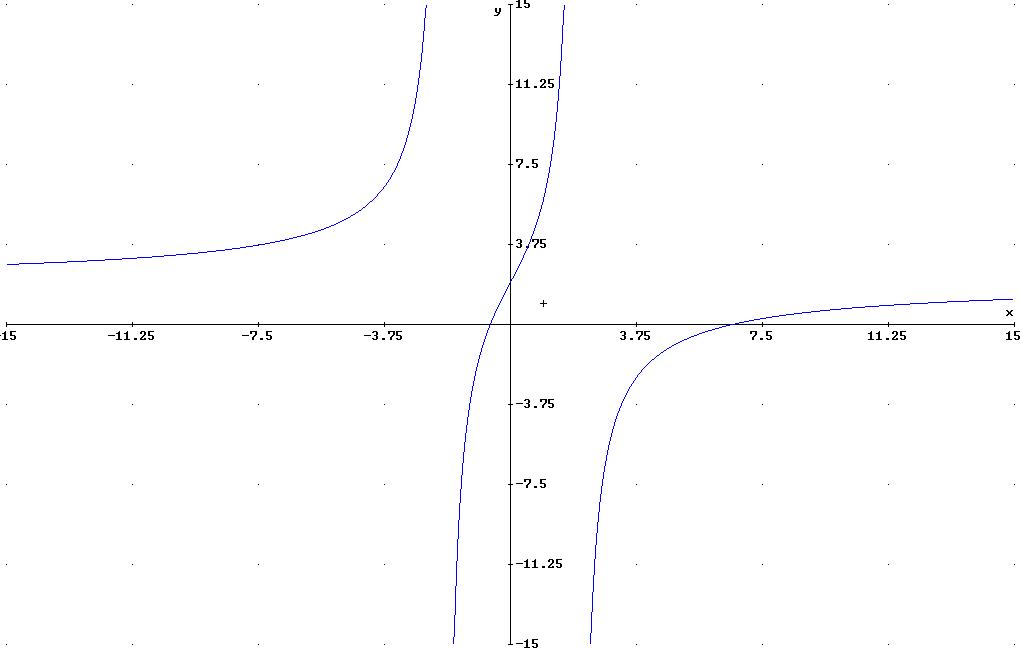raphik:

Gegebenen ist eine Funktion, welche durch die Punkte A und B verläuft. Ermitteln Sie die Parameter a,b,c und führen Sie anschließend eine vollständige Kurvendiskussion durch.

Einsetzen der Punkte A und B in die Ausgangsgleichung:

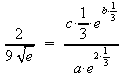
Gleichungen dividieren: Kürzen und zusammenfassen:

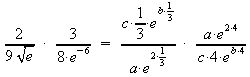
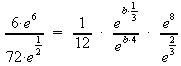
Potenzen zusammenfassen (Potenzen mit gleichen Basen werden dividiert, indem man ihre Exponenten subtrahiert):

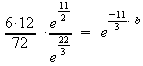
Einsetzen des Parameters b in eine der beiden Gleichungen:

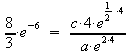
Die Funktion mit eingesetzten Parametern lautet also:

Jetzt kann eine Kurvendiskussion durchgeführt werden:

Definitionsbereich:

Achsenschnittpunkte: y-Achse x=0

x-Achse y=0

Ableitungen:

=

=

lokale Extrema:

hinreichende Bedingung:

Wendestellen:

hinreichende Bedingung:

Symmetrie: keine Symmetrie

Monotonie: x1=0.6 monoton steigend

x2=0.7 monoton fallend

Verhalten im Unendlichen:

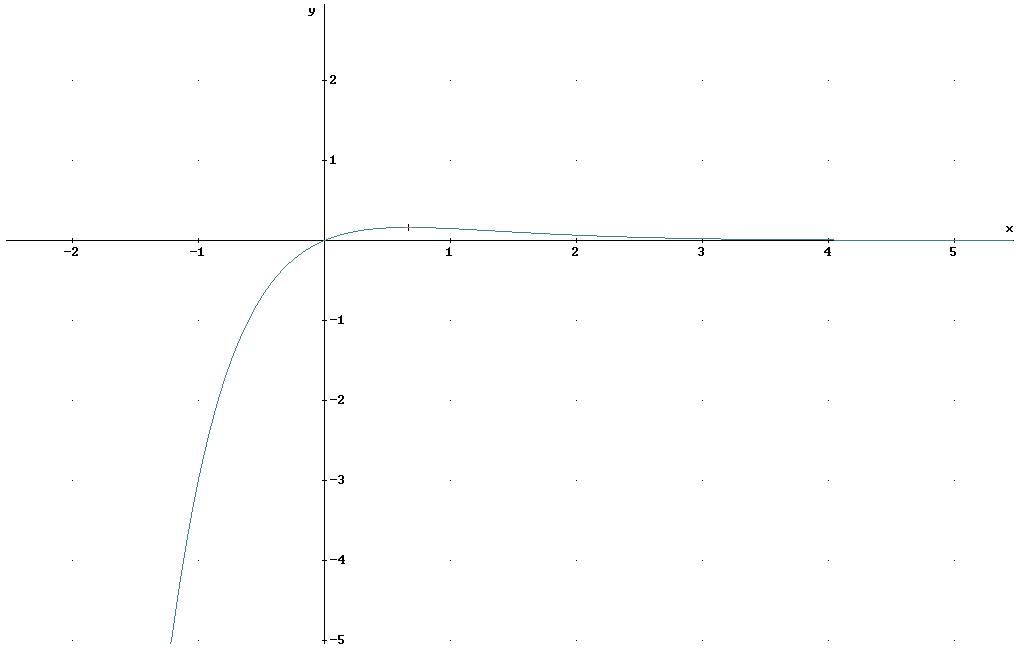
Graphik: