Führen Sie für folgende Funktion eine Kurvendiskussion durch:

Definitionsbereich:

Achsenschnittpunkte:

y-Achse: PY [0/0]

X-Achse:

PX1 [0/0]

PX1 [-0.5/0]

Ableitungen:

Extrema:

EP1[0/0]

Finden der Nullstelle durch Probieren:

für x= -0.5 -0.5

für x= +0.5 +3.79

Erste Schätzung: x= -0.3

NEWTON`SCHES NÄHERUNGSVERFAHREN:

EP2[-0.3474702/0.0321457]

hinreichende Bedingung prüfen:

Wendestelle:

Finden der Nullstelle durch Probieren:

für x=-0.3-0.6

für x= 0.01.38

Erste schätzung: x= -0.2

NEWTON`SCHES NÄHERUNGSVERFAHREN:

WP [-0.186923/0.0169886]

hinreichende Bedingung prüfen:

Verhalten im Unendlichen:

Monotonie:

Symmetrie:

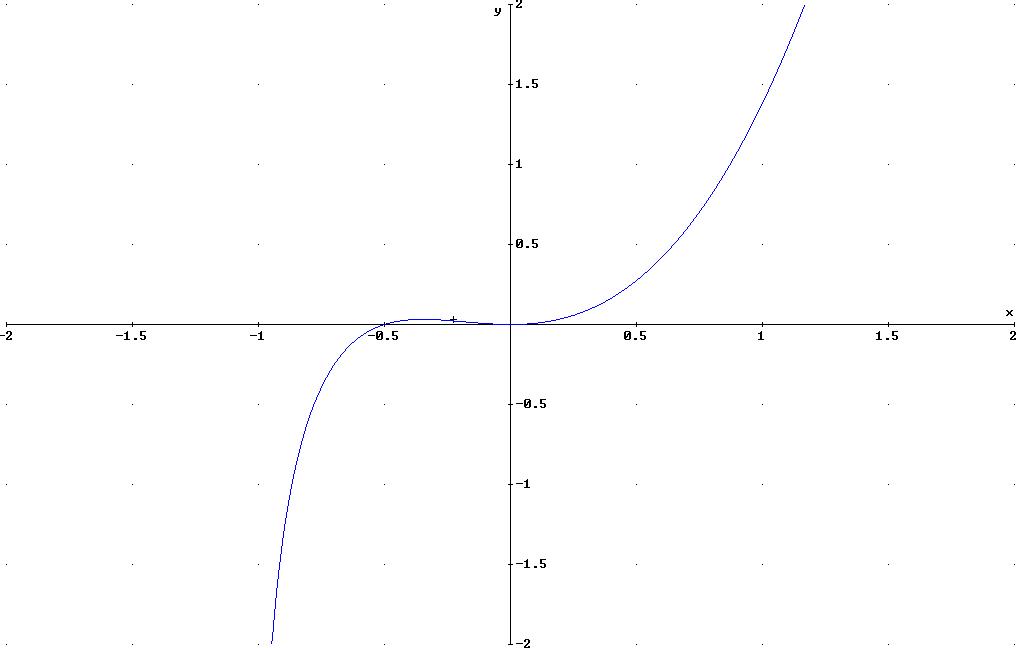
Graphik:

Führen Sie für folgende Funktion eine Kurvendiskussion durch:

Definitionsbereich:

Achsenschnittpunkte:

Y-Achse: PY [0/0]

X-Achse: PX1 [0/0]

PX2 [1.25/0]

Ableitungen:

=

=

=

Extrema:

lösen nach p-q-Formel:

hinreichende Bedingung prüfen:

EP1 [1.925905/0.1106014] EP2 [0.3246095/-0.6277605]

Wendestellen:

lösen nach p-q-Formel: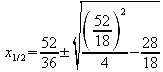

hinreichende Bedingung prüfen:

WP1 [2.1730487/0.1039604] WP2 [0.7158402/-0.3654066]

Verhalten im Unendlichen:

Monotonie:

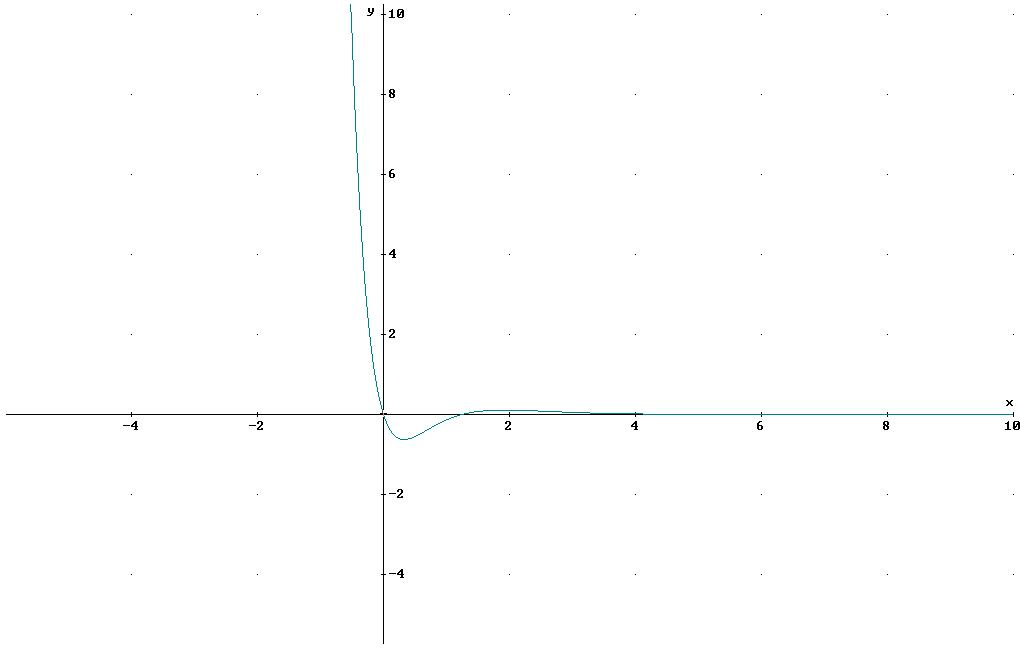
Symmetrie:

Graphik: