DIE PARTIELLE INTEGRATION
Die Integration eines Produktes von Funktionen ist nicht einfach, für das Verfahren verwenden wir die Produktregel der Differentialrechnung.
Überlegungen für unbestimmte Integrale:
Die Ableitung der Stammfunktion F(x)= u(x) v(x) dx ist die Ausgangsfunktion
f(x)= u(x) v'(x) + u'(x) v(x). Durch Integration erhält man daraus:
Da
,
folgt:
|
BEDINGUNGEN:
u,v
im Intervall (a,b) differenzierbar
u',v'
im Intervall (a,b) stetig
Die Anwendung dieses Satzes nennt man „partielle Integration“, um anzudeuten, dass ein Restintegral bleibt. Man integriert nur teilweise – „partiell“. Dieses Restintegral ist entweder ein uns bekanntes Grundintegral oder muss weiter bearbeitet werden.
1.BEISPIEL:
im Intervall (0,4)
ableiten:
integrieren:
In die obige Formel einsetzen:
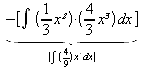
[ x^6 Potenzen zusammenfassen ]
Damit gilt:
=
4987.26 FE
2.BEISPIEL:
v=-x
v'=-1
u'=cosx
u=
sinx
ZU BEACHTEN: Die Funktion, die nach mehrmaligem Ableiten Null wird, ist immer die Funktion v(x)!
Einsetzen in die formel der partiellen Integration:
PROBE:
=
Das kontrollierende Differenzieren am Ende bestätigt das Ergebnis, die beiden letzten Terme entfallen und es bleibt die Ausgangsfunktion: (-x cosx)
3.BEISPIEL:
v=x
v'=1
u'=
u=
Beim
unbestimmten Integrieren, z.B. von
muss
man die innere Ableitung beachten. Denn beim Differenzieren entsteht
ein störender Faktor:
f(x)
=
f'(x)
=
Um
den Faktor bei der gegenläufigen Operation aufzuheben,lautet die
innere Integration
.
PROBE:
Der erste und der dritte Term heben sich auf und im zweiten kürzen sich die 2en weg, somit ist auch dieses ergebnis eindeutig bestätigt.
4.BEISPIEL: DIE DREIFACHE PARTIELLE INTEGRATION
3.Teil:
v=
v'=
u'=
u=
=
PROBE:
Erster und dritter Term heben sich auf.
=
PROBE:
Erster und vierter, dritter und fünfter Term heben sich auf.
1.Teil:
-
PROBE:
Erster/ Vierter,dritter/sechster,fünfter/siebenter Term heben sich auf.
v=
v'=
u'=
u=
2.Teil:
v=
v'=
u'=
u=
-